
Клеточные автоматы
1. ОСНОВНЫЕ ПОНЯТИЯ
Современные компьютеры стали мощным инструментом для научных исследований в самых разных областях. Очень распространено моделирование, то есть исследование информационных моделей с использованием компьютеров. Одним и методов компьютерного моделирования является исследование так называемых клеточных автоматов. С их помощью можно смоделировать самые различные объекты и процессы; от процесса образования галактик до распространения инфекционных заболеваний и развития колонии микроорганизмов.

Рис. 1. Моделирование распространения инфекционного заболевания

Риc. 2. Моделирование распространения тепла
1.1. Устройство плоского клеточного автомата
Представим себе плоскость, разбитую на квадратные клетки. Каждая клетка имеет характеристику называемую ее состоянием. Состояние обозначается числом, а при отображении клеточного автомата на экране – определенным цветом, обозначающим это число. Если число, обозначающее состояние клетки может принимать любое значение в каком-либо диапазоне, автомат называется автоматом с непрерывным множеством состояний. Так на рис.3 показаны клетки с состояниями 0; 0,3; 0,7; 1. Они отображаются разной степенью почернения клетки от 0 - чисто белый цвет до 1 – черный.

Рис. 3
Очевидно, что определенная степень серого цвета отображает состояние клетки – десятичную дробь с любой требуемой точностью.

Рис. 4. Изменение состояния клетки отображается степенью почернения клетки от 0 (белый) до 1 (черный)
Если состояние обозначается целыми числами, автомат называется дискретным. Для отображения состояний его клеток используют контрастные цвета. Например, для отображения восьми состояний клеток автомата используют таблицу типа:
Таблица 1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Белый
|
Синий
|
Зеленый
|
Красный
|
Желтый
|
Серый
|
Коричневый
|
Черный
|

Рис.5. Отображение состояния клетки цветом
Частным случаем дискретного автомата является автомат с состояниями клеток 0 или 1. Такой автомат называют бинарным. На экране состояния клеток такого автомата обозначают:
0- белым цветом, 1 – черным цветом.
1.2. Окрестность клетки. Состояние окрестности
Каждая клетка клеточного автомата соседствует с некоторыми другими клетками. Эти клетки образуют окрестность клетки. Различают два вида окрестности:
окрестность Неймана, она состоит из четырех соседних клеток;
окрестность Мура, она состоит из восьми соседних клеток.
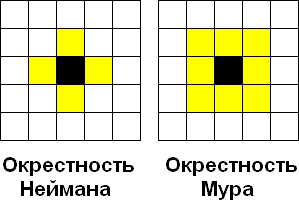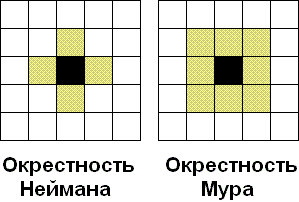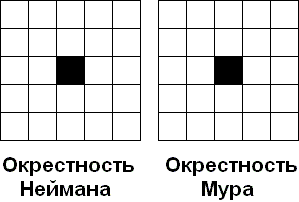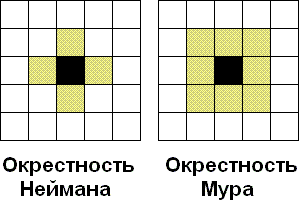
Рис. 6. Окрестности клетки
Состоянием окрестности клетки называют число – сумму состояний клеток окрестности. Так для бинарного клеточного автомата состояние окрестности Неймана может быть {0, 1, 2, 3, 4}, а окрестности Мура – {0, 1, 2, 3, 4, 5, 6, 7, 8}. Для дискретного автомата с количеством состояний n состояние окрестности – целое число от 0 до n*4 (окрестность Неймана) или целое число от 0 до n*8 (окрестность Мура). Для автомата с непрерывным множеством состояний состояние окрестности может принимать дробное значение от 0 до 4 для окрестности Неймана и от 0 до 8 для окрестности Мура.
1.3. Мощность клеточного автомата. Положение клетки. Граничные клетки
Теоретически плоскость, разбитая на клетки может быть бесконечной. Практически же всегда имеют дело с ограниченным количеством клеток. Обычно это квадрат из клеток. Количество клеток клеточного автомата называется его мощностью. На рис. 7 показан бинарный клеточный автомат с мощностью 12*12=144 клеток.
Положение каждой клетки характеризуется двумя числами – координатами. Так на рис. 7 изображен бинарный клеточный автомат, у которого самая верхняя клетка с состоянием 1 (черная) имеет координаты (4,2), а самая нижняя с таким же состоянием – координаты (7,10).
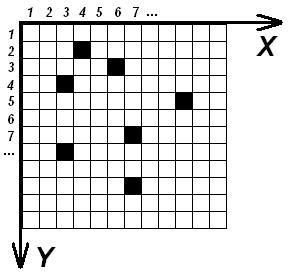
Рис. 7. Координаты клеток
Чем больше клеток в этом квадрате, тем совершеннее клеточная модель, но и тем труднее она в реализации на компьютере. Поэтому всегда приходят к компромиссу, например, используют клеточный автомат с размером квадрата 100*100, то есть из 10000 клеток.
Особое положение занимают клетки на границах квадрата. У них окрестность содержит меньшее количество клеток, чем клетки внутри квадрата. Это создает трудности при реализации клеточной модели. Для их преодоления используют два приема:
используют только те клетки, которые находятся вдалеке от границы квадрата;
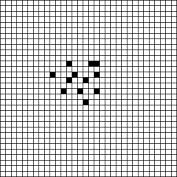
Рис.8
квадрат «сворачивают» в тор («бублик»), при этом все клетки будут иметь «правильную» окрестность.
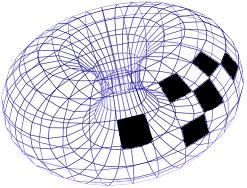
Рис. 9
1.4. Состояние клеточного автомата. Такт. Закон изменения состояния клетки. Жизненный цикл клеточного автомата
Информация о состоянии всех клеток клеточного автомата называется состоянием клеточного автомата. Обычно состояние клеточного автомата хранится в двумерном массиве типа k(n,n), где n – размер стороны квадрата. Для экономии оперативной памяти и увеличении скорости счета состояний клеточного автомата можно хранить только ненулевые значения состояний клеток. Так для клеточного автомата на рис.7 его состояние – это значения элементов массива: k (2,4)=1; k(3,6)=1; k(4,3)=1; k(5,10)=1; k(7,7)=1; k(8,3)=1; k(10,7). Остальные клетки (их количество 144-7=137) имеют состояние 0.
Тактом называется процедура определения для всех клеток состояния их окрестностей и назначение каждой клетке нового состояния в зависимости от состояния ее окрестности. При этом используют закон изменения состояния клетки. Этот закон является основной характеристикой клеточного автомата. После определения нового состояния каждой клетки осуществляется переход в следующий такт и весь процесс повторяется. Количество тактов определяет жизненный цикл клеточного автомата.
Начальным состоянием клеточного автомата называется описание состояния всех его клеток на первом такте. Обычно все клетки кроме небольшого числа (может быть только одной клетки) получают начальное состояние 0.
Если на каком-либо такте все клетки принимают одинаковое значение (например, нулевое), жизненный цикл может быть досрочно прерван. Его прерывают и в том случае, когда при переходе на следующий такт состояния всех клеток не изменяется.
«Конструирование» клеточного автомата (будем обозначать его КА) происходит так:
назначают мощность КА;
устанавливают закон изменения состояния клетки;
назначают множество состояний клеток;
назначают состояния некоторых клеток, отличное от 0 (начальное состояние КА);
устанавливают жизненный цикл КА.
Далее сконструированный КА «запускают», то есть просчитываются состояния окрестности каждой клетки, назначаются новые состояния, снова просчитываются состояния на новом такте и т. д. пока не окончится жизненный цикл. Состояние КА в конце жизненного цикла называется конечным состоянием.
1.5. Возможности клеточного автомата
Очень многие физические, биологические, социальные процессы могут быть смоделированы клеточным автоматами. В самом деле, если представить сообщество людей как клетки, состояния которых будут характеризовать состояние здоровья человека (можно в виде двух состояний: 0 – здоровый, 1 – больной), а окрестностью считать тех людей, с которыми контактирует человек, то можно смоделировать процесс распространения инфекционного заболевания (см. рис. 1).
Образование планет из околозвездного пылевого облака можно смоделировать клеточным автоматом, у которого состояние клетки будет обозначать плотность материи в определенном объеме пространства. Закон изменения состояния клеток будет описывать процесс гравитационного взаимодействия близких масс газопылевого облака при образовании планет.
Различные биологические процессы моделируются клеточными автоматами. Например, процесс развития зародыша из одной оплодотворенной клетки заключается в последовательном делении клеток. При этом происходит взаимодействие соседних клеток и осуществляется их дифференциация (изменение вида). Так образуются специализированные клетки многоклеточного организма (нервные, клетки кожного покрова, внутренних органов и пр.).
Вперед >>
Сайт создан в системе
uCoz







