3. ПЛОСКИЙ КЛЕТОЧНЫЙ АВТОМАТ УЛАМА

  • Американский математик Станислав Улам предложил КА со следующими параметрами:

    каждая клетка может иметь состояние 0 или 1 (бинарный КА);

    окрестность клетки состоит из четырех клеток (окрестность Неймана);

    закон изменения состояния клетки:

    1. Если состояние клетки 0, а состояние ее окрестности 1, ее состояние на следующем такте будет 1.

    2. Во всех остальных случаях состояние клетки на следующем такте 0.

  • Попробуем вручную просчитать состояния КА Улама при начальном состоянии всех клеток 0 за исключение единственной клетки с состоянием 1.

    Рис. 12

  • Для исследования КА Улама используется программа Ulam.exe , В ней используется 101*101=10201 клетка. Начальное состояние 1 присваивается нужному количеству клеток по их координатам x, y, затем КА «запускается». Интересно наблюдать, как происходит взаимодействие клеток, при этом образуются достаточно сложные конфигурации. Так из всего двух клеток состояния 1 с координатами (50,55) и (47,40) начального состояния КА образуется на 64 такте состояние, показанное на рис. 13.

    Рис.13 (программа ulam)

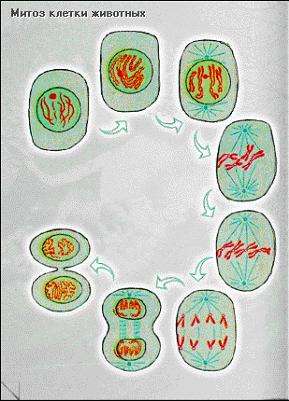
  • Клеточный автомат Улама имеет еще одно интересное свойство – копирование исходных структур. Задав начальное состояние клеток в виде некоторой структуры, через определенное число тактов получаем четыре их копии. При этом процесс очень напоминает то, который наблюдают под микроскопом при делении (митозе) живых клеток.

    Рис. 14. Митоз клетки

    Рис. 15. Копирование структуры КА Улама (программа copy)

  • << Назад***Вперед >>

    Сайт создан в системе uCoz